Decision Tree#
Note
Decision tree split node by one feature at each step.
ID3 split according to information gain.
C4.5 split according to information gain ratio.
CART split according to square error & gini.
Pruning tries to minimize leaves entropy and model’s complexity at the same time.
Information Gain ID3#
Suppose we have a classification problem, dataset \(D=\{(x^{(1)}, y^{(1)}),...,(x^{(n)}, y^{(n)})\}\), \(y^{(i)} \in \left\{1,...,k\right\}\).
Then the entropy of \(D\) which measures uncertainty:
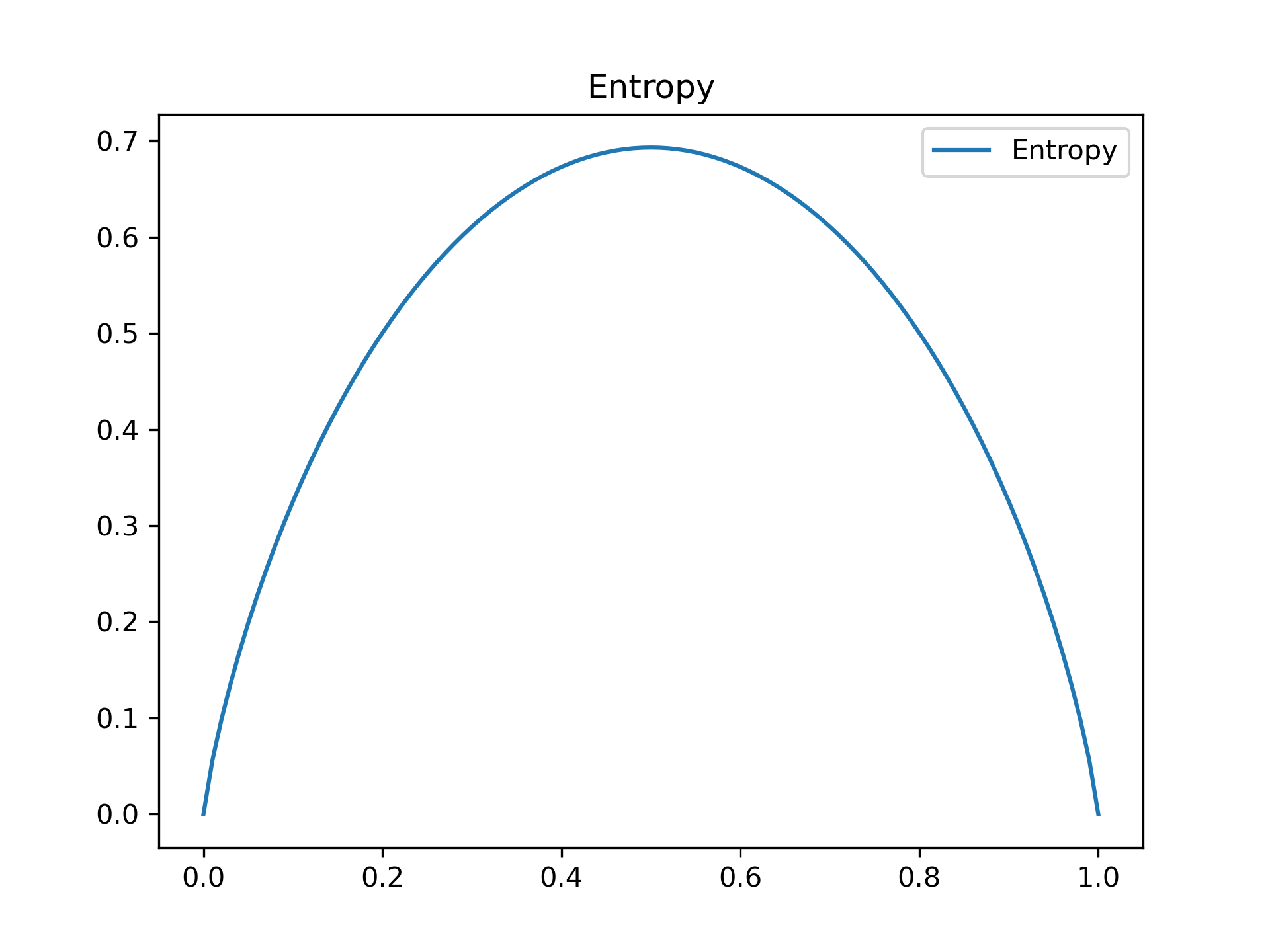
Assume we partition \(D\) according to feature \(A\) into \(D_{1},...,D_{m}\), then the entropy of \(D\) after knowing \(A\):
Information gain is uncertainty loss:
Decision Tree ID3 choose feature \(A\) that maximize \(g(D,A)\) until:
subset is empty
information gain \(g(D,A)\le\epsilon\)
Information Gain Ratio C4.5#
Information gain prefer feature \(A\) such that \(\#A\) is large, more precisely,
is large.
Information gain ratio fix this by dividing \(H_{A}(D)\):
CART-classification and regression tree#
For regression problem, we try to find feature \(j\) and cutting point \(s\) that minimize the square error:
For classification problem CART uses gini:
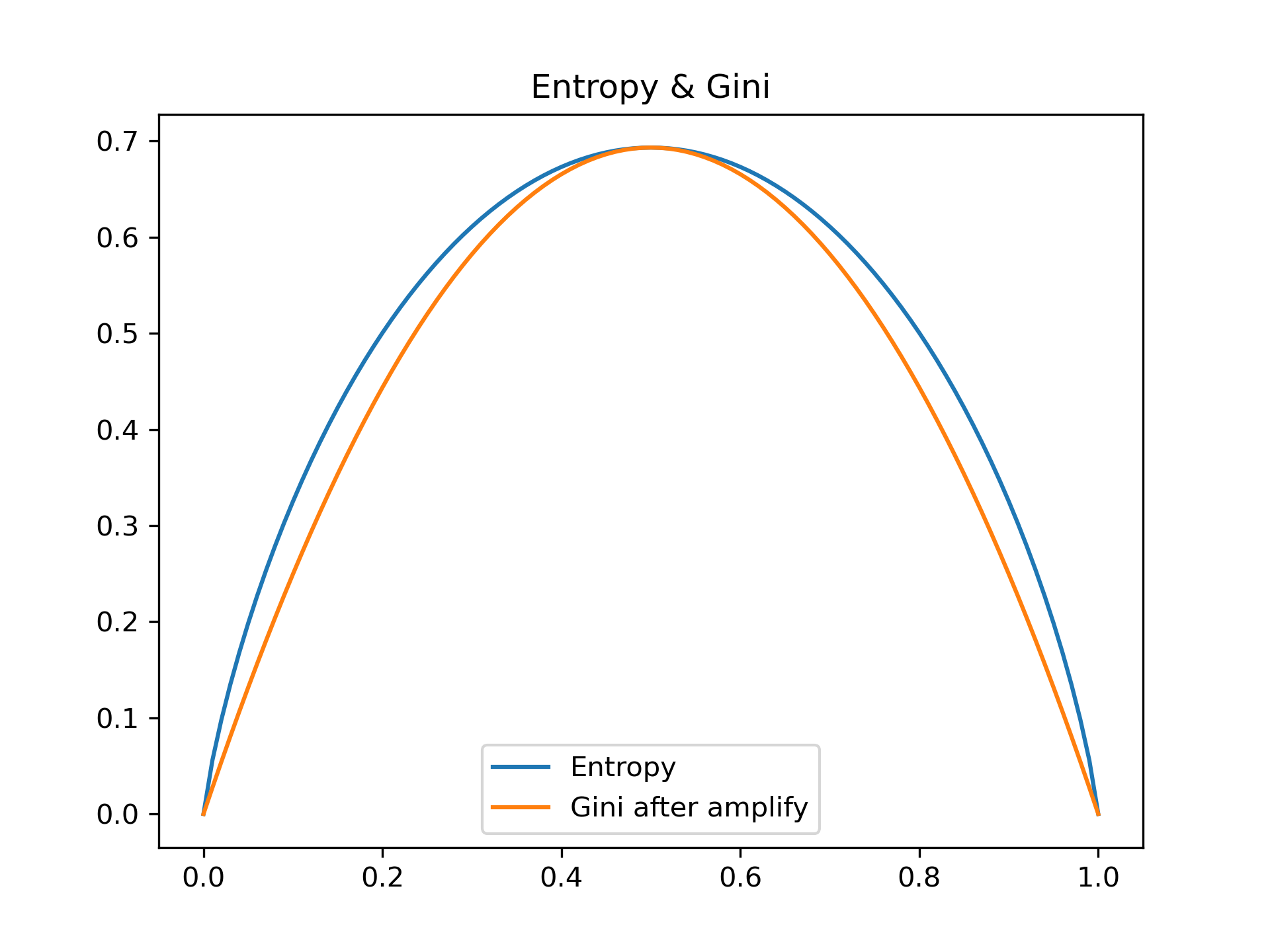
Pruning#
Total entropy of these leaves:
We want to minimize this entropy, and at the same time limit model’s complexity.
Loss function:
If pruning a node result in a decrease of the loss function, then pruning the node.
Examples#
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
"""hyperparameters"""
from sklearn.tree import DecisionTreeClassifier
tree_clf = DecisionTreeClassifier(criterion="entropy", # default gini
# maximum depth of that tree
max_depth=3,
# maximum number of leaf nodes
max_leaf_nodes=15,
# maximum number of features when splitting each node
max_features=2,
# min number of samples of a node before it can split
min_samples_split=8,
# min number of samples of a leaf node
min_samples_leaf=3,
# same as min_samples_leaf, but by weight frac
min_weight_fraction_leaf=0.01)
tree_clf.fit(X, y)
DecisionTreeClassifier(criterion='entropy', max_depth=3, max_features=2,
max_leaf_nodes=15, min_samples_leaf=3,
min_samples_split=8, min_weight_fraction_leaf=0.01)
"""visualize using graphviz, need 1.pip install graphviz, 2.brew install graphviz"""
from graphviz import Source
from sklearn.tree import export_graphviz
export_graphviz(tree_clf,
out_file="iris_tree.dot",
feature_names=iris.feature_names[2:],
class_names=iris.target_names,
rounded=True,
filled=True
)
Source.from_file("iris_tree.dot")
Grid Search#
from sklearn.model_selection import GridSearchCV
param_grid = [{"max_leaf_nodes": [2, 5], "min_samples_split": [3, 4]}]
clf = DecisionTreeClassifier()
grid_search = GridSearchCV(clf, param_grid, cv=3, verbose=3)
grid_search.fit(X, y)
grid_search.best_estimator_
Fitting 3 folds for each of 4 candidates, totalling 12 fits
[CV] max_leaf_nodes=2, min_samples_split=3 ...........................
[CV] max_leaf_nodes=2, min_samples_split=3, score=0.660, total= 0.0s
[CV] max_leaf_nodes=2, min_samples_split=3 ...........................
[CV] max_leaf_nodes=2, min_samples_split=3, score=0.660, total= 0.0s
[CV] max_leaf_nodes=2, min_samples_split=3 ...........................
[CV] max_leaf_nodes=2, min_samples_split=3, score=0.660, total= 0.0s
[CV] max_leaf_nodes=2, min_samples_split=4 ...........................
[CV] max_leaf_nodes=2, min_samples_split=4, score=0.660, total= 0.0s
[CV] max_leaf_nodes=2, min_samples_split=4 ...........................
[CV] max_leaf_nodes=2, min_samples_split=4, score=0.660, total= 0.0s
[CV] max_leaf_nodes=2, min_samples_split=4 ...........................
[CV] max_leaf_nodes=2, min_samples_split=4, score=0.660, total= 0.0s
[CV] max_leaf_nodes=5, min_samples_split=3 ...........................
[CV] max_leaf_nodes=5, min_samples_split=3, score=0.980, total= 0.0s
[CV] max_leaf_nodes=5, min_samples_split=3 ...........................
[CV] max_leaf_nodes=5, min_samples_split=3, score=0.920, total= 0.0s
[CV] max_leaf_nodes=5, min_samples_split=3 ...........................
[CV] max_leaf_nodes=5, min_samples_split=3, score=0.960, total= 0.0s
[CV] max_leaf_nodes=5, min_samples_split=4 ...........................
[CV] max_leaf_nodes=5, min_samples_split=4, score=0.980, total= 0.0s
[CV] max_leaf_nodes=5, min_samples_split=4 ...........................
[CV] max_leaf_nodes=5, min_samples_split=4, score=0.940, total= 0.0s
[CV] max_leaf_nodes=5, min_samples_split=4 ...........................
[CV] max_leaf_nodes=5, min_samples_split=4, score=1.000, total= 0.0s
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 0.0s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 2 out of 2 | elapsed: 0.0s remaining: 0.0s
[Parallel(n_jobs=1)]: Done 12 out of 12 | elapsed: 0.0s finished
DecisionTreeClassifier(max_leaf_nodes=5, min_samples_split=4)
